Curvilinear Interpolation using HARK’s CurvilinearInterp class

Johns Hopkins University
Econ-ARK

This notebook uses examples from scipy documentation to demonstrate HARK’s Warped2DInterp class.

from __future__ import annotations

from time import time

import matplotlib.pyplot as plt
import numpy as np
from HARK.interpolation import Curvilinear2DInterp

from multinterp.curvilinear import Warped2DInterp

Suppose we have a collection of values for an unknown function along with their respective coordinate points. For illustration, assume the values come from the following function:

def function_1(x, y):
    return x * (1 - x) * np.cos(4 * np.pi * x) * np.sin(4 * np.pi * y**2) ** 2

The points are randomly scattered in the unit square and therefore have no regular structure.

rng = np.random.default_rng(0)
warp_factor = 0.01
x_list = np.linspace(0, 1, 20)
y_list = np.linspace(0, 1, 20)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_1(rand_x, rand_y)

Now suppose we would like to interpolate this function on a rectilinear grid, which is known as “regridding”.

grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 100), np.linspace(0, 1, 100), indexing="ij"
)

To do this, we use HARK’s Warped2DInterp class. The class takes the following arguments:

  • values: an ND-array of values for the function at the points
  • grids: a list of ND-arrays of coordinates for the points
  • method: the interpolation method to use, with options WarpedInterp, “linear”, “cubic” (for 2D only), and “rbf”. The default is 'linear'.
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")
warped_interp.warmup()

Once we create the interpolator objects, we can use them using the __call__ method which takes as many arguments as there are dimensions.

start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00253 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.01309 seconds

Now we can compare the results of the interpolation with the original function. Below we plot the original function and the sample points that are known.

plt.imshow(function_1(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin="lower")
plt.plot(rand_x.flat, rand_y.flat, "ok", ms=2, label="input points")
plt.title("Original")
plt.legend(loc="lower right")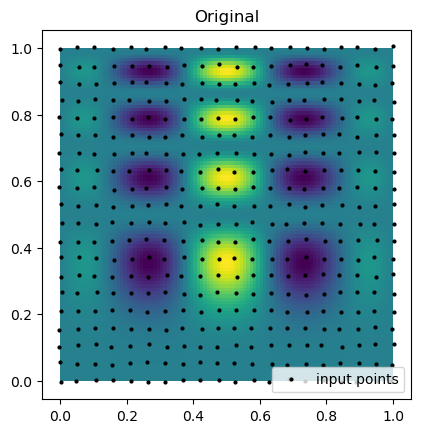
<Figure size 640x480 with 1 Axes>

Then, we can look at the result for each method of interpolation and compare it to the original function.

fig, axs = plt.subplots(1, 3, figsize=(9, 6))
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_1(grid_x, grid_y), warped_grid, curvilinear_grid]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid.T, extent=(0, 1, 0, 1), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()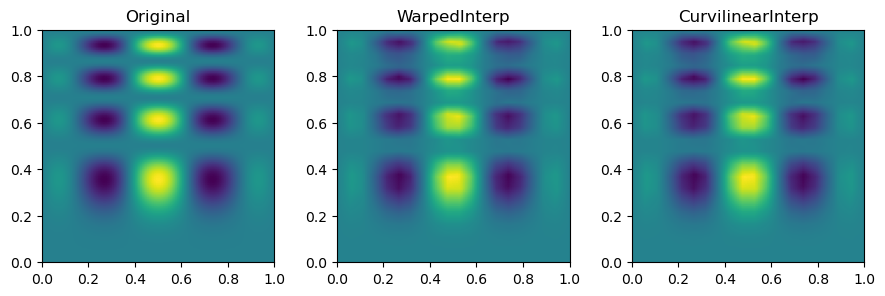
<Figure size 900x600 with 3 Axes>

Another Example

def function_2(x, y):
    return np.hypot(x, y)
rng = np.random.default_rng(0)
warp_factor = 0.05
x_list = np.linspace(-0.5, 0.5, 10)
y_list = np.linspace(-0.5, 0.5, 10)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_2(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(-0.5, 0.5, 100), np.linspace(-0.5, 0.5, 100), indexing="ij"
)
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")

start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00100 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.00652 seconds

plt.imshow(function_2(grid_x, grid_y), extent=(-0.5, 0.5, -0.5, 0.5), origin="lower")
plt.plot(rand_x.flat, rand_y.flat, "ok", ms=2, label="input points")
plt.title("Original")
plt.legend(loc="lower right")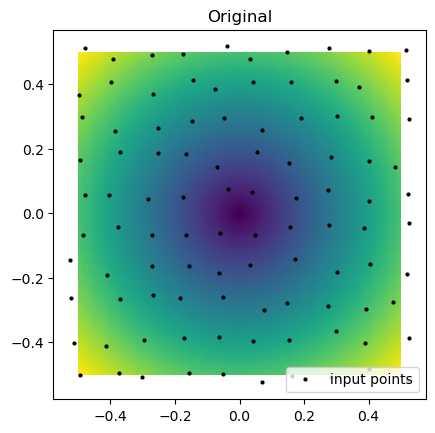
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(1, 3, figsize=(10, 3))
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_2(grid_x, grid_y), warped_grid, curvilinear_grid]

for _i, (ax, title, grid) in enumerate(zip(axs.flat, titles, grids)):
    im = ax.pcolormesh(grid_x, grid_y, grid, shading="auto")
    ax.set_title(title)

cbar = fig.colorbar(im, ax=axs)
for ax in axs.flat:
    ax.axis("equal")

plt.show()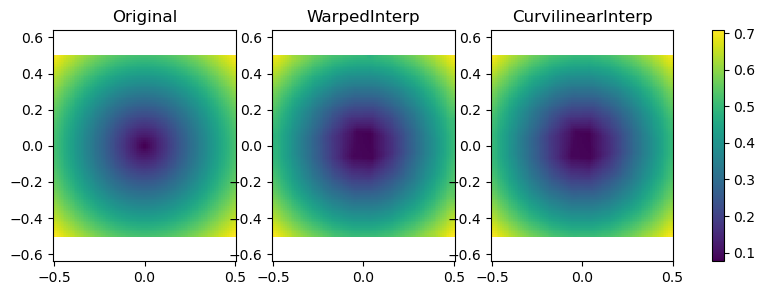
<Figure size 1000x300 with 4 Axes>

Unstructured Interpolators with Curvilinear Grids

def function_3(u, v):
    return u * np.cos(u * v) + v * np.sin(u * v)
rng = np.random.default_rng(0)
warp_factor = 0.1
x_list = np.linspace(0, 3, 10)
y_list = np.linspace(0, 3, 10)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_3(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 3, 100), np.linspace(0, 3, 100), indexing="ij"
)
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")
start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00100 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.00704 seconds

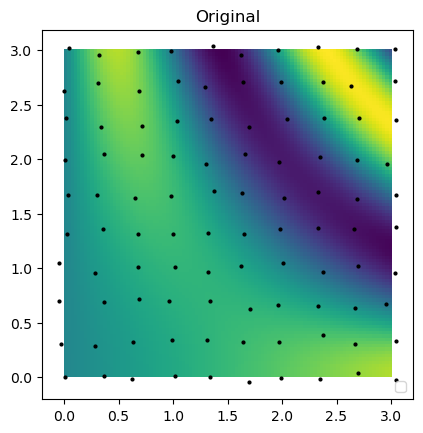
plt.imshow(function_3(grid_x, grid_y).T, extent=(0, 3, 0, 3), origin="lower")
plt.plot(rand_x.flat, rand_y.flat, "ok", ms=2)
plt.title("Original")
plt.legend(loc="lower right")
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(1, 3, figsize=(9, 3))
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_3(grid_x, grid_y), warped_grid, curvilinear_grid]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid, extent=(0, 3, 0, 3), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()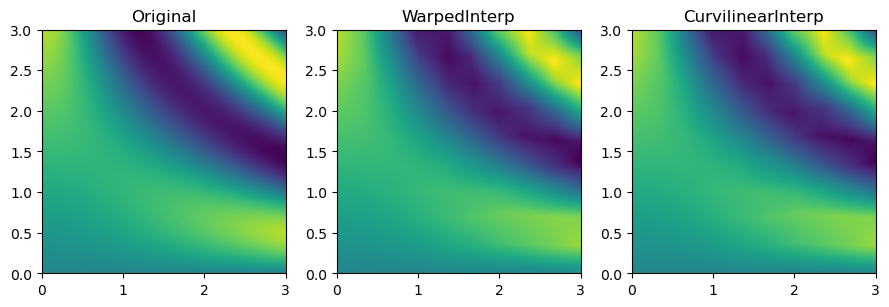
<Figure size 900x300 with 3 Axes>
def function_4(x, y):
    return 3.0 * x**2.0 + x * y + 4.0 * y**2.0
rng = np.random.default_rng(0)
warp_factor = 0.2
x_list = np.linspace(0, 5, 10)
y_list = np.linspace(0, 5, 10)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_4(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 5, 100), np.linspace(0, 5, 100), indexing="ij"
)
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")
start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00100 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.00854 seconds

plt.imshow(function_4(grid_x, grid_y).T, extent=(0, 5, 0, 5), origin="lower")
plt.plot(rand_x, rand_y, "ok", ms=2)
plt.title("Original")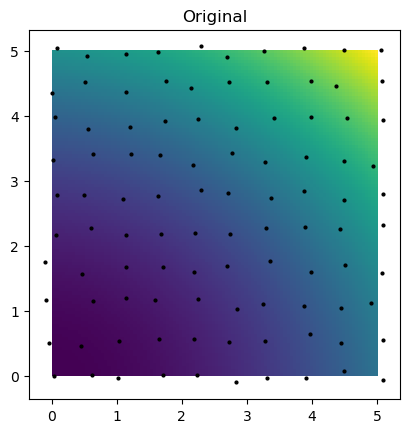
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(1, 3, figsize=(9, 3))
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_4(grid_x, grid_y), warped_grid, curvilinear_grid]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid, extent=(0, 3, 0, 3), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()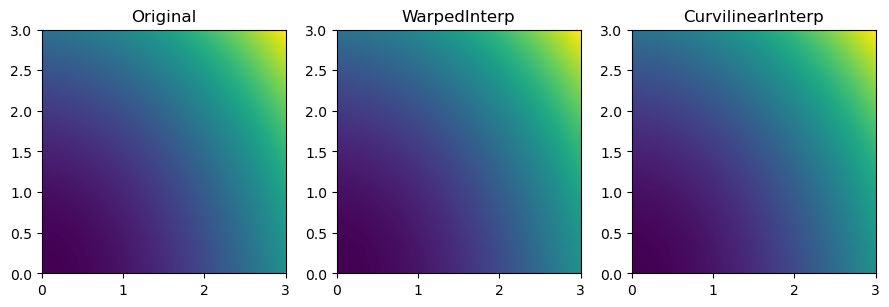
<Figure size 900x300 with 3 Axes>

More complex functions

def function_5(*args):
    return np.maximum(
        0.0,
        1.0
        - np.exp(0.5 - np.prod(np.asarray(args) + 0.2, axis=0) ** (1.0 / len(args))),
    )
rng = np.random.default_rng(0)
warp_factor = 0.05
x_list = np.linspace(0, 1, 25)
y_list = np.linspace(0, 1, 25)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_5(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 100), np.linspace(0, 1, 100), indexing="ij"
)
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")
start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00100 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.02109 seconds

c:\Users\alujan\micromamba\envs\multinterp-dev\Lib\site-packages\HARK\interpolation.py:4243: RuntimeWarning: invalid value encountered in sqrt
  alpha = (-eta + polarity * np.sqrt(eta**2.0 - 4.0 * zeta * theta)) / (

ax = plt.axes(projection="3d")
ax.plot_surface(
    grid_x,
    grid_y,
    function_5(grid_x, grid_y),
    rstride=1,
    cstride=1,
    cmap="viridis",
    edgecolor="none",
)
ax.scatter(rand_x, rand_y, values, c=values, cmap="viridis", label="input points")
plt.title("Original")
plt.legend(loc="lower right")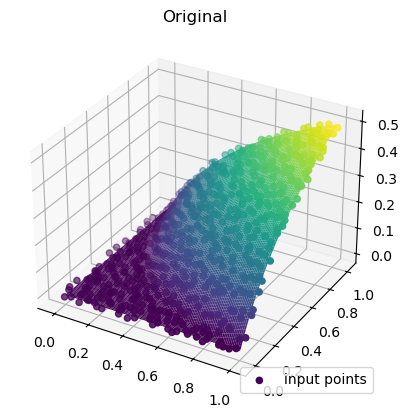
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(1, 3, figsize=(9, 3), subplot_kw={"projection": "3d"})
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_5(grid_x, grid_y), warped_grid, curvilinear_grid]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.plot_surface(
        grid_x, grid_y, grid, rstride=1, cstride=1, cmap="viridis", edgecolor="none"
    )
    ax.set_title(title)

plt.tight_layout()
plt.show()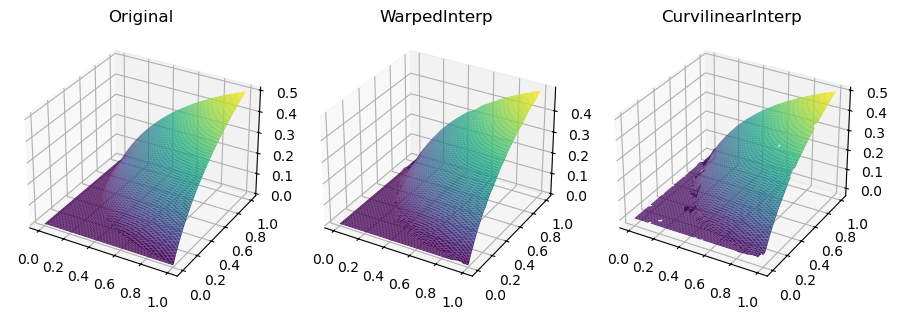
<Figure size 900x300 with 3 Axes>
def function_6(x, y):
    return 1 / (np.abs(0.5 - x**4 - y**4) + 0.1)
rng = np.random.default_rng(0)
warp_factor = 0.05
x_list = np.linspace(0, 1, 25)
y_list = np.linspace(0, 1, 25)
x_temp, y_temp = np.meshgrid(x_list, y_list, indexing="ij")
rand_x = x_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
rand_y = y_temp + warp_factor * (rng.random((x_list.size, y_list.size)) - 0.5)
values = function_6(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 100), np.linspace(0, 1, 100), indexing="ij"
)
warped_interp = Warped2DInterp(values, (rand_x, rand_y), backend="numba")
start = time()
warped_grid = warped_interp(grid_x, grid_y)
print(f"Warped interpolation took {time() - start:.5f} seconds")
Warped interpolation took 0.00202 seconds

curvilinear_interp = Curvilinear2DInterp(values, rand_x, rand_y)
start = time()
curvilinear_grid = curvilinear_interp(grid_x, grid_y)
print(f"Curvilinear interpolation took {time() - start:.5f} seconds")
Curvilinear interpolation took 0.02110 seconds

ax = plt.axes(projection="3d")
ax.plot_surface(
    grid_x,
    grid_y,
    function_6(grid_x, grid_y),
    rstride=1,
    cstride=1,
    cmap="viridis",
    edgecolor="none",
)
ax.scatter(rand_x, rand_y, values, c=values, cmap="viridis", label="input points", s=1)
ax.view_init(30, 150)
plt.title("Original")
plt.legend(loc="lower right")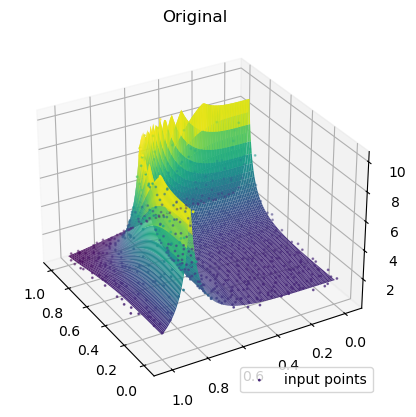
<Figure size 640x480 with 1 Axes>
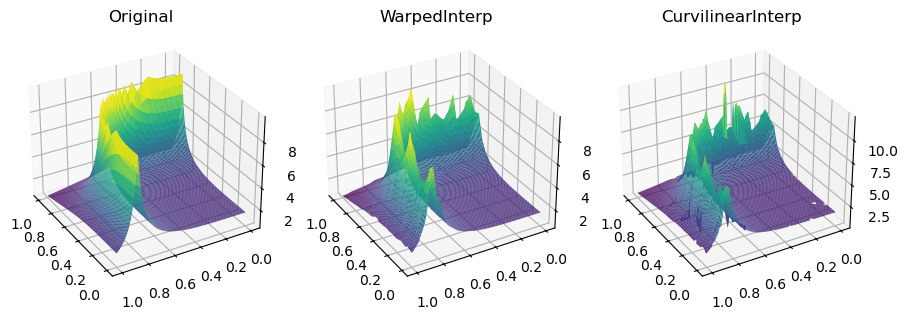
fig, axs = plt.subplots(1, 3, figsize=(9, 3), subplot_kw={"projection": "3d"})
titles = ["Original", "WarpedInterp", "CurvilinearInterp"]
grids = [function_6(grid_x, grid_y), warped_grid, curvilinear_grid]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.plot_surface(
        grid_x, grid_y, grid, rstride=1, cstride=1, cmap="viridis", edgecolor="none"
    )
    ax.set_title(title)
    ax.view_init(30, 150)

plt.tight_layout()
plt.show()
<Figure size 900x300 with 3 Axes>
Curvilinear
Warped Interpolation
Curvilinear
Piecewise Affine Interpolation