Regression Interpolation using scikit-learn

Johns Hopkins University
Econ-ARK

This notebook uses examples from scipy documentation to demonstrate HARK’s UnstructuredInterp class.

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np

from multinterp.unstructured import RegressionUnstructuredInterp

Suppose we have a collection of values for an unknown function along with their respective coordinate points. For illustration, assume the values come from the following function:

def func(x, y):
    return x * (1 - x) * np.cos(4 * np.pi * x) * np.sin(4 * np.pi * y**2) ** 2

The points are randomly scattered in the unit square and therefore have no regular structure.

rng = np.random.default_rng(0)
rand_x, rand_y = rng.random((2, 1000))
values = func(rand_x, rand_y)

Now suppose we would like to interpolate this function on a rectilinear grid, which is known as “regridding”.

grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 100), np.linspace(0, 1, 100), indexing="ij"
)

To do this, we use HARK’s UnstructuredInterp class. The class takes the following arguments:

  • values: an ND-array of values for the function at the points
  • grids: a list of ND-arrays of coordinates for the points
  • method: the interpolation method to use, with options “nearest”, “linear”, “cubic” (for 2D only), and “rbf”. The default is 'linear'.
elastic_net_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="elastic-net", std=True
)
elastic_net_cv_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="elastic-net-cv", std=True
)
kernel_ridge_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="kernel-ridge", std=True
)
svr_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="svr", std=True
)
sgd_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="sgd", std=True
)
gaussian_interp = RegressionUnstructuredInterp(
    values, (rand_x, rand_y), model="gaussian-process", std=True
)

Once we create the interpolator objects, we can use them using the __call__ method which takes as many arguments as there are dimensions.

elastic_net_grid = elastic_net_interp(grid_x, grid_y)
elastic_net_cv_grid = elastic_net_cv_interp(grid_x, grid_y)
kernel_ridge_grid = kernel_ridge_interp(grid_x, grid_y)
svr_grid = svr_interp(grid_x, grid_y)
sgd_grid = sgd_interp(grid_x, grid_y)
gaussian_grid = gaussian_interp(grid_x, grid_y)

Now we can compare the results of the interpolation with the original function. Below we plot the original function and the sample points that are known.

plt.imshow(func(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin="lower")
plt.plot(rand_x, rand_y, "ok", ms=2, label="input points")
plt.title("Original")
plt.legend(loc="lower right")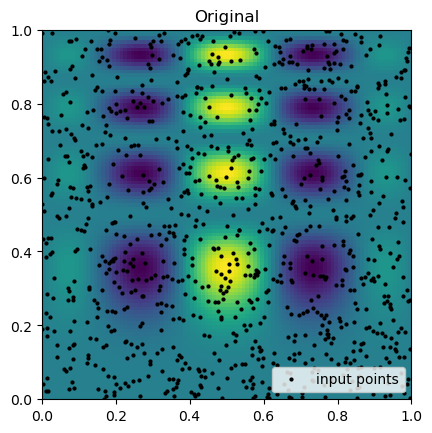
<Figure size 640x480 with 1 Axes>

Then, we can look at the result for each method of interpolation and compare it to the original function.

fig, axs = plt.subplots(3, 2, figsize=(6, 6))
titles = [
    "Elastic Net",
    "Elastic Net CV",
    "Kernel Ridge",
    "SVR",
    "SGD",
    "Gaussian Process",
]
grids = [
    elastic_net_grid,
    elastic_net_cv_grid,
    kernel_ridge_grid,
    svr_grid,
    svr_grid,
    gaussian_grid,
]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid.T, extent=(0, 1, 0, 1), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()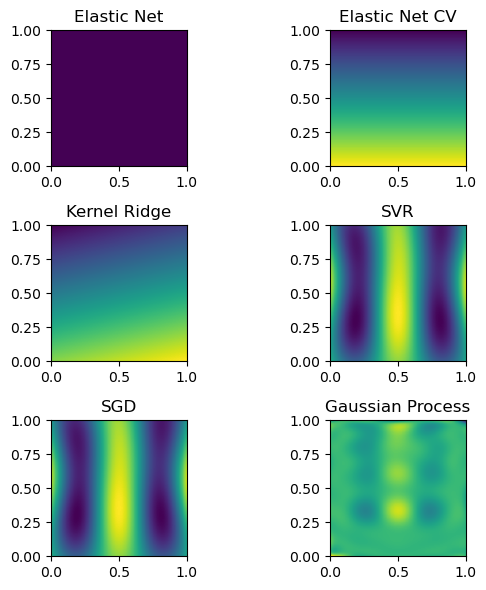
<Figure size 600x600 with 6 Axes>

Another Example

rng = np.random.default_rng(0)
rand_x = rng.random(20) - 0.5
rand_y = rng.random(20) - 0.5
values = np.hypot(rand_x, rand_y)
grid_x = np.linspace(min(rand_x), max(rand_x))
grid_y = np.linspace(min(rand_y), max(rand_y))
grid_x, grid_y = np.meshgrid(grid_x, grid_y)  # 2D grid for interpolation
elastic_net_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net",
)
elastic_net_cv_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net-cv",
)
kernel_ridge_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="kernel-ridge",
)
svr_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="svr",
)
sgd_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="sgd",
)
gaussian_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="gaussian-process",
)
elastic_net_grid = elastic_net_interp(grid_x, grid_y)
elastic_net_cv_grid = elastic_net_cv_interp(grid_x, grid_y)
kernel_ridge_grid = kernel_ridge_interp(grid_x, grid_y)
svr_grid = svr_interp(grid_x, grid_y)
sgd_grid = sgd_interp(grid_x, grid_y)
gaussian_grid = gaussian_interp(grid_x, grid_y)
plt.imshow(np.hypot(grid_x, grid_y).T, extent=(-0.5, 0.5, -0.5, 0.5), origin="lower")
plt.plot(rand_x, rand_y, "ok", label="input points")
plt.title("Original")
plt.legend(loc="lower right")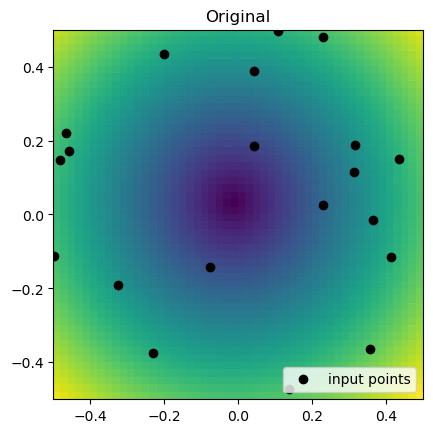
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(3, 2, figsize=(6, 6))
titles = [
    "Elastic Net",
    "Elastic Net CV",
    "Kernel Ridge",
    "SVR",
    "SGD",
    "Gaussian Process",
]
grids = [
    elastic_net_grid,
    elastic_net_cv_grid,
    kernel_ridge_grid,
    svr_grid,
    svr_grid,
    gaussian_grid,
]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid.T, extent=(0, 1, 0, 1), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()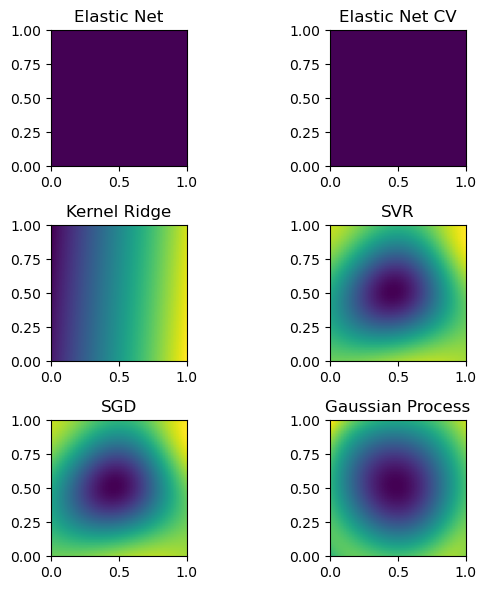
<Figure size 600x600 with 6 Axes>

Unstructured Interpolators with Rectilinear Grids

def F(u, v):
    return u * np.cos(u * v) + v * np.sin(u * v)
rand_x, rand_y = np.meshgrid(
    np.linspace(0, 3, 10), np.linspace(0, 3, 10), indexing="ij"
)
values = F(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 3, 100), np.linspace(0, 3, 100), indexing="ij"
)
elastic_net_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net",
)
elastic_net_cv_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net-cv",
)
kernel_ridge_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="kernel-ridge",
)
svr_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="svr",
)
sgd_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="sgd",
)
gaussian_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="gaussian-process",
)
elastic_net_grid = elastic_net_interp(grid_x, grid_y)
elastic_net_cv_grid = elastic_net_cv_interp(grid_x, grid_y)
kernel_ridge_grid = kernel_ridge_interp(grid_x, grid_y)
svr_grid = svr_interp(grid_x, grid_y)
sgd_grid = sgd_interp(grid_x, grid_y)
gaussian_grid = gaussian_interp(grid_x, grid_y)
plt.imshow(F(grid_x, grid_y).T, extent=(0, 3, 0, 3), origin="lower")
plt.plot(rand_x, rand_y, "ok", ms=2)
plt.title("Original")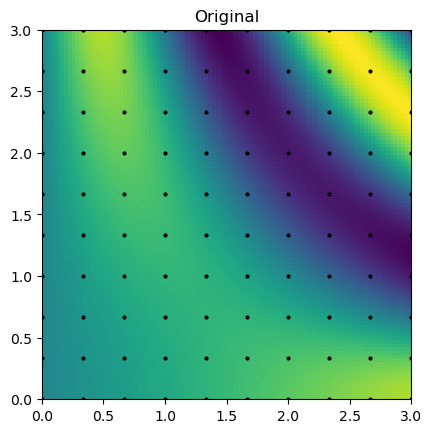
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(3, 2, figsize=(6, 6))
titles = [
    "Elastic Net",
    "Elastic Net CV",
    "Kernel Ridge",
    "SVR",
    "SGD",
    "Gaussian Process",
]
grids = [
    elastic_net_grid,
    elastic_net_cv_grid,
    kernel_ridge_grid,
    svr_grid,
    svr_grid,
    gaussian_grid,
]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.imshow(grid.T, extent=(0, 1, 0, 1), origin="lower")
    ax.set_title(title)

plt.tight_layout()
plt.show()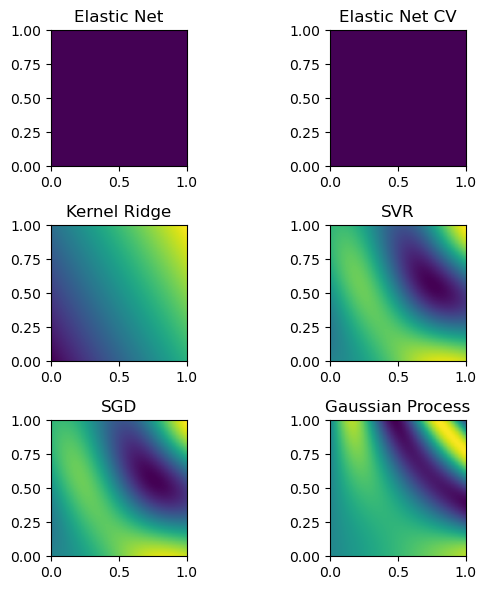
<Figure size 600x600 with 6 Axes>

More complex functions

def f_d(*args):
    return np.maximum(
        0.0,
        1.0
        - np.exp(0.5 - np.prod(np.asarray(args) + 0.2, axis=0) ** (1.0 / len(args))),
    )
rng = np.random.default_rng(0)
rand_x, rand_y = rng.random((2, 500))
values = f_d(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 50), np.linspace(0, 1, 50), indexing="ij"
)
elastic_net_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net",
)
elastic_net_cv_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net-cv",
)
kernel_ridge_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="kernel-ridge",
)
svr_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="svr",
)
sgd_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="sgd",
)
gaussian_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="gaussian-process",
)
original_grid = f_d(grid_x, grid_y)
elastic_net_grid = elastic_net_interp(grid_x, grid_y)
elastic_net_cv_grid = elastic_net_cv_interp(grid_x, grid_y)
kernel_ridge_grid = kernel_ridge_interp(grid_x, grid_y)
svr_grid = svr_interp(grid_x, grid_y)
sgd_grid = sgd_interp(grid_x, grid_y)
gaussian_grid = gaussian_interp(grid_x, grid_y)
ax = plt.axes(projection="3d")
ax.plot_surface(
    grid_x,
    grid_y,
    original_grid,
    rstride=1,
    cstride=1,
    cmap="viridis",
    edgecolor="none",
)
ax.scatter(rand_x, rand_y, values, c=values, cmap="viridis", label="input points")
plt.title("Original")
plt.legend(loc="lower right")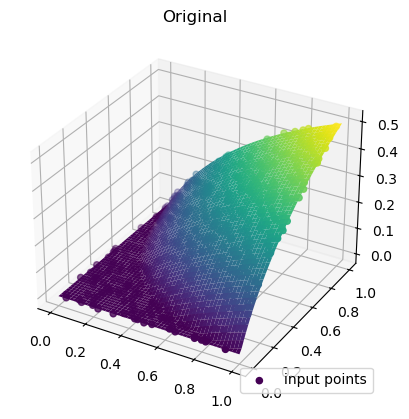
<Figure size 640x480 with 1 Axes>
fig, axs = plt.subplots(3, 2, figsize=(6, 6), subplot_kw={"projection": "3d"})
titles = [
    "Elastic Net",
    "Elastic Net CV",
    "Kernel Ridge",
    "SVR",
    "SGD",
    "Gaussian Process",
]
grids = [
    elastic_net_grid,
    elastic_net_cv_grid,
    kernel_ridge_grid,
    svr_grid,
    svr_grid,
    gaussian_grid,
]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.plot_surface(
        grid_x, grid_y, grid, rstride=1, cstride=1, cmap="viridis", edgecolor="none"
    )
    ax.set_title(title)

plt.tight_layout()
plt.show()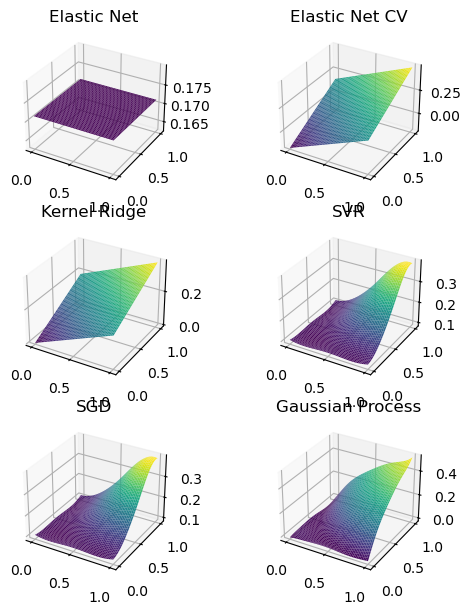
<Figure size 600x600 with 6 Axes>
def f_d(x, y):
    return 1 / (np.abs(0.5 - x**4 - y**4) + 0.1)
rng = np.random.default_rng(0)
rand_x, rand_y = rng.random((2, 1000))
values = f_d(rand_x, rand_y)
grid_x, grid_y = np.meshgrid(
    np.linspace(0, 1, 100), np.linspace(0, 1, 100), indexing="ij"
)
elastic_net_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net",
)
elastic_net_cv_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="elastic-net-cv",
)
kernel_ridge_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="kernel-ridge",
)
svr_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="svr",
)
sgd_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="sgd",
)
gaussian_interp = RegressionUnstructuredInterp(
    values,
    (rand_x, rand_y),
    model="gaussian-process",
    pp_options={"feature": "spline"},
)
original_grid = f_d(grid_x, grid_y)
elastic_net_grid = elastic_net_interp(grid_x, grid_y)
elastic_net_cv_grid = elastic_net_cv_interp(grid_x, grid_y)
kernel_ridge_grid = kernel_ridge_interp(grid_x, grid_y)
svr_grid = svr_interp(grid_x, grid_y)
sgd_grid = sgd_interp(grid_x, grid_y)
gaussian_grid = gaussian_interp(grid_x, grid_y)
ax = plt.axes(projection="3d")
ax.plot_surface(
    grid_x,
    grid_y,
    original_grid,
    rstride=1,
    cstride=1,
    cmap="viridis",
    edgecolor="none",
)
ax.scatter(rand_x, rand_y, values, c=values, cmap="viridis", label="input points")
ax.view_init(30, 150)
plt.title("Original")
plt.legend(loc="lower right")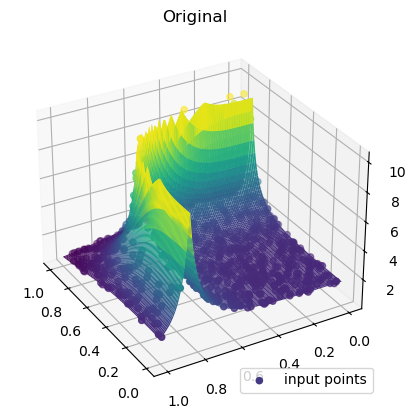
<Figure size 640x480 with 1 Axes>
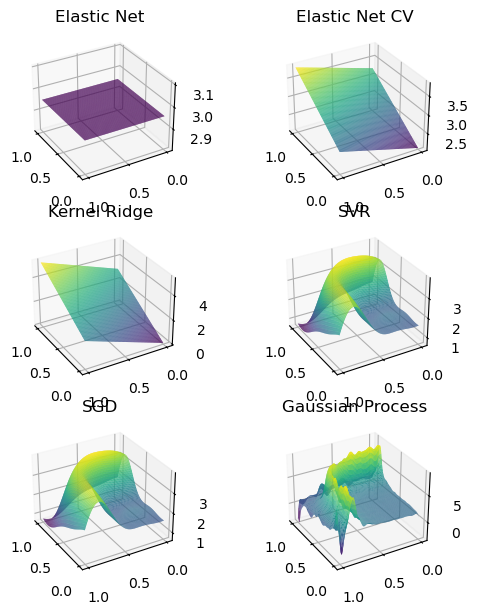
fig, axs = plt.subplots(3, 2, figsize=(6, 6), subplot_kw={"projection": "3d"})
titles = [
    "Elastic Net",
    "Elastic Net CV",
    "Kernel Ridge",
    "SVR",
    "SGD",
    "Gaussian Process",
]
grids = [
    elastic_net_grid,
    elastic_net_cv_grid,
    kernel_ridge_grid,
    svr_grid,
    svr_grid,
    gaussian_grid,
]

for ax, title, grid in zip(axs.flat, titles, grids):
    im = ax.plot_surface(
        grid_x, grid_y, grid, rstride=1, cstride=1, cmap="viridis", edgecolor="none"
    )
    ax.set_title(title)
    ax.view_init(30, 150)

plt.tight_layout()
plt.show()
<Figure size 600x600 with 6 Axes>
Unstructured
Unstructured Interpolation using scipy
Unstructured
gpytorch